Scientists should acknowledge the limitations of their method and the limitations of the results they are presenting up front and not wait for the defense to develop the concept (if they even know to do so).

What should attorneys know about significant digits or figures?

It is all about superfluous precision.  To a non-technical person, a measurement seems to be really powerful if it has a lot of digits after the zero.

Think about this example…

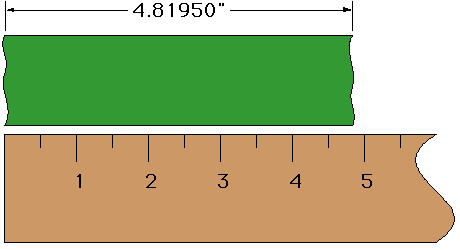
Wow the green object is 4.81950 inches!  Sounds really precise and exacting, doesn’t it?  But the truth is that due to the unevenness of the object and the coarseness of the ruler, the best we can say is the length is about 4.8 inches.  Reporting anything other than this about 4.8 inches (ignoring for the moment the large and important concept of uncertainty budgeting) is misleading as it implies the measurement is precise and exact to 5 decimal places.

This is where the concept of “significant figures” come into play.

For example, the population of a city might only be known to the nearest thousand and be stated as 42,000, while the population of a country might only be known to the nearest million and be stated as 42,000,000. The former might be in error by hundreds, and the latter might be in error by hundreds of thousands, but both have two significant figures (4 and 2). This reflects the fact that the significance of the error (its likely size relative to the size of the quantity being measured) is the same in both cases.

Well how does this typically happen?

Spurious digits introduced, for example, by calculations carried out to greater accuracy than that of the original data, or measurements reported to a greater precision than the equipment supports.

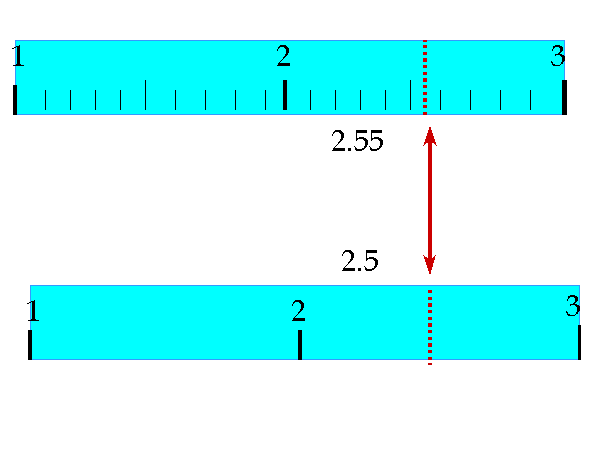
Think about this in the sense of accident scene reconstruction where speed is the crucial measurement sought to be discovered and calculated.  This is often derived from length measures.  This is where your measurement device and its significant digits can be crucial.  It can lead to erroneous answers otherwise.

The Two Greatest Sources of Error Regarding Significant Digits

1. Writing more digits in an answer (intermediate or final) than justified by the number of digits in the data.
2. Rounding-off, say, to two digits in an intermediate answer, and then writing three digits in the final answer.

We cannot ignore significant digits.