The concept of a match at first look blush seems rather elemental.  However, if we really were to think of it, the concept is indeed fungible.  In forensic science, there is no universally held definition across all disciplines or even within a disciple as to what constitutes sufficient similarity to evoke that coveted and magic word:  “match”.

It seems to me that a good working definition of the word “match” ought to be something such as the two items examined are so unique to one another that it excludes all other explanations.  That is unique.  No other possibility of error.  In a word “identical”.

The problem in practice as opposed to theory can be summed up in four basic questions:

1. How closely do we look?
2. How do we look?
3. What do we use as a method of comparison?
4. How sure can we be?

In this post, we will illustrate how in practice the concept of “match” is really an illusion.

The problem is best illustrated by the phenomenon correctly called Random Match Probability Error or RMPE.  It is otherwise known simply as “The Birthday Problem”.

In probability theory, the birthday problem, or birthday paradox pertains to the probability that in a set of randomly chosen people some pair of them will have the same birthday (matching criteria=when only month and day is examined—not including year, hour or second). In a group of at least 23 randomly chosen people, there is more than 50% probability that some pair of them will have the same birthday. Such a result (for just 23 people, considering that there are 365 possible birthdays) is counter-intuitive to many.

How hard is it in a room full of strangers to find:

• Someone born on the same month as you?  Is that a match?
• Someone born on the same month and day?  Is that a match?
• Someone born on the same month, day and year?  Is that a match?
• Someone born on the same month, day, year and hour?  Is that a match?
• Someone born on the same month, day, year, hour and second?  Is that a match?
• Someone born on the same month, day, year, hour, second and state?  Is that a match?
• Someone born on the same month, day, year, hour, second, state and city?  Is that a match?
• Someone born on the same month, day, year, hour, second, state, city and hospital?  Is that a match?
• Someone born on the same month, day, year, hour, second, state, city, hospital and room?  Is that a match?

For 57 or more people, the probability is more than 99%, and it reaches 100% when the number of people reaches 366 (ignoring leap years). The mathematics behind this problem led to a well-known cryptographic attack called the birthday attack.

Let’s examine the beloved and often praised science of DNA.  Even the National Academy of Science’s earth shattering report praised DNA science above all other science.  However, is such praise worthy?

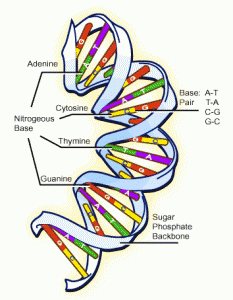
The problem comes when one tries to do base pairing and what the examiner uses as a criteria is for a “match”.  What is your method of analysis:  STR versus LCN?  How many base pairs versus all possible base pairs?  Some forensic labs are alarmingly low in their matching criteria.

Think of the Birthday problem.  If you change the “matching criteria” from the birthday (when only month and year is examined—not including year, hour or second) and you switch it to a more meaningful metric such as month, day, year, hour, second, state, city, hospital, room and floor, then the chances of finding a match in a room substantially and radically changes.

So, we need to be careful and not call something a match.