If you haven’t noticed a theme in these blog posts, it is really quite simple:

1. Exposing limitations of assays.
2. Showing the interpretive parts of forensic science

I also admit that I love metrology as it should be applied to forensic science.

As I have written before:

I have blogged before on metrology and Uncertainty Measurement (UM).  Even the mighty International Standard, ISO 17025, in Section 5.4.6 only applies the concept of UM to the quantitative measure and hence results not a true expression of the Bayesian-based expanded uncertainty budget.  In order to do so, it must also must be an expression of the uncertainty in the qualitative measure as well to be truly metrologically responsible.

In another post I asked and examined the key question of:

What is the use of expressing uncertainty in the quantitative result if we are not as scientifically sure as possible of what we in fact measuring?

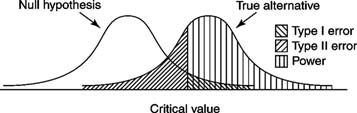
The importance of identifying and establishing the Type I and Type II error in Bayesian-based metrology is that if done correctly, it can result in discovering the true “power” of the assay.

Type I and Type II errors are inversely related:  As one increases, the other decreases.  The Type I, or α (alpha), error rate is usually set in advance by the researcher.  The Type II error rate for a given test is harder to know because it requires estimating the distribution of the alternative hypothesis, which is usually unknown.

Power is the probability that a test will reject the null hypothesis when it is, in fact, false.  You can see from the below figure, power is simply 1 minus the Type II error rate (β).  High power is desirable.  Like β, power can be difficult to estimate accurately, but increasing the sample size always increases power.

Boiling point….

Assume that we were to use boiling point to distinguish between unknown substances.  The boiling points are normally distributed with a mean of 480 degrees and a standard deviation of 5 degrees, and the boiling points  of a counterfeit substance are normally distributed with a mean of 465 degrees  and a standard deviation of 7 degrees. Assume also that 90% of the substances are genuine, hence 10% are counterfeit.
What is the probability that a randomly chosen genuine substance has a boiling point more than 475 grains?
What is the probability that a randomly chosen counterfeit substance has a boiling point more than 475 grains?
What is the probability that a randomly chosen substance has a boiling point more than 475 degrees  and is genuine?
What is the probability that a randomly chosen substance has a boiling point more than 475 degrees  and is counterfeit?
What is the probability that a randomly chosen substance which has a boiling point more than 475 degrees is genuine?

These and more are the questions that need to be answered in forensic science.  What is the power of your assay?  Stop reporting analytical chemistry as single number and as an absolute!